Laws of size reduction
- The estimation of the power
requirement of crushing and grinding operations are very important in the
design and selection of size reduction equipment
- But it is not possible to estimate
accurately the power requirement of crushing and grinding to affect the
size reduction of a given material.
- There are a number of
empirical laws to find power requirement crushing and grinding
operations
Rittinger's law
It states that the work required for the crushing operation is directly proportional to the newly generated surface area.
- Mathematically
- where
P= power
required by the machine
m = feed rate
to machine
Kr =
Rittinger's constant
Kick's law
- Kick's law related the energy
to the sizes of the feed particles and the product particles
It states that the work required for crushing a given material is proportional to the logarithm of the ratio between the initial and final diameters
- where
KK
= Kick's constant
D and d =
initial and final diameters
- Kick's law is more accurate than
Rittinger's law for the course where the amount of surface produced is
considerably less.
Bond's law
- Bond has proposed a law
intermediate between Rittinger's and kick's law for estimating the power
required for crushing and grinding operations.
Bond postulated that work required to form particles of size Dp from the very large feed is proportional to the square root of the surface-to-volume ratio of the product, Sp/Vp.
- By relation Sp/Vp
= 6/ɸsDp, from which it follows that
- where
Dp =
the particle size
Kb = Bond's
constant that depends on the type of machine and the material being crushed
Hence Bond's law also states that the total work useful in breakage is inversely proportional to the square root of the diameter of the product particles.
- from above equation, a work index
Wi is defined as the gross energy required in kilowatt-hours
per ton of feed material, required to reduce a very large feed to such a
size that 80 % of the product passes a 100-µm screen.
- This definition leads to a
relation between Kb and Wi. If Dp is in
millimeters, P in kilowatts, and ṁ in tons per hour
- If 80% of the feed passes a mesh
size of Dpa millimeters and 80% of the product passes through a
mesh of Dpb millimeters, then from above two equation we get

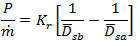








No comments:
Post a Comment